El modelo de Solow-Swan es muy conocido por su aplicación en tópicos como teoría de crecimiento el cual busca explicar el crecimiento de los países bajo supuestos como funciones de producción (mayormente neoclásicas), economías sin gobierno, donde además se supone que el trabajo crece a la misma tasa que la población, el capital (K) se deprecia cada periodo a tasa constante ∈[0,1]
** Recordar que la producción en funciones de producción neoclásicas presenta rendimientos constantes a escala, su productividad marginal es positiva y decreciente y satisface condiciones INADA
Las condiciones INADA según Sala-i-Martin (1990) señala que la producción marginal del capital se aproxima a cero cuando esta tienda a infinito y cuando tienda a al infinito el capital se aproxime a cero.
Ecuación fundamental
Así también es preciso mencionar que las tasas de crecimiento de las variables per cápita como el cápita, ingreso, consumo en estado estacionario tienen un crecimiento igual a cero
Regla de Oro , Phelps(1961): La regla de oro busca maximizar el consumo per cápita respecto a respecto al capital con lo cual podemos hallar el capital de estado estacionario:
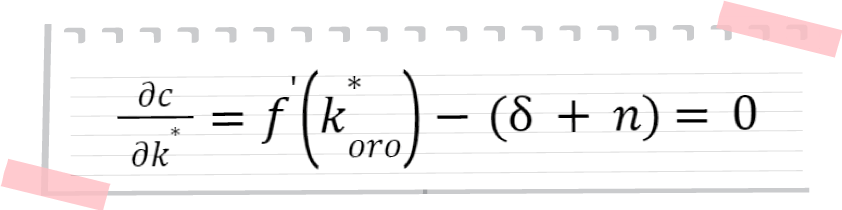
Por tanto, se puede determinar una tasa de ahorro óptima a la cual la economía deberá crecer a fin evitar desbalances como el sobre ahorro y desahorro.
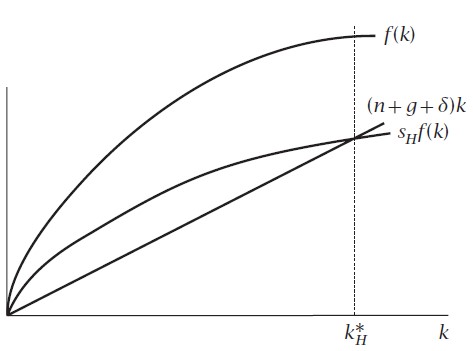
Concluyendo que la acumulación de capital no es la clave del crecimiento, sin embargo, si dicho modelo incorporásemos el progreso tecnológico podemos afirmar que el modelo es la única fuente de crecimiento sostenido del stock de capital per cápita.
Referencias:
Phelps, E.(1961). The Golden Rule of Accumulation: A Fable for Growthmen, The American Economic Review, 51(4), 638-643.
Sala-i-Martin (1990). Apuntes de crecimiento económico, Antoni Bosch Editor.
Si te gusto este blog, mira todo el contenido que tenemos para tí...
